\[ \]

Numerical Intergration and Simpson's Rule

Issue No 65, 3 March 2025

By: Anthony O. Ives

Integration was introduced in an earlier article [1]. One of the most useful applications of integration is determining areas or volumes specifically if you know the mathematical relationships of the bounding curves. However, this article looks at using numerical methods, which makes it possible for anyone even if you hate mathematical equations and integration to determine areas or volumes by simply taking a set of measurements around your odded shaped area or volume.

As explained in the earlier article [1] integration is really the reverse of differentiation [2] and has many usefully applications. However, you may have used integration without knowing it, specifically numerical integration. This article should also give a good explaination of numerical methods in general and that it is a simple process to solve a complicated problem. In this case our complicated problem will be determining the area of an unusual shape.

Numerical integration can be described simply by splitting your unusual shape into a series of even width strips and then working out the approximate area of each by assuming they are rectriangles. See picture below for illustration of the process:

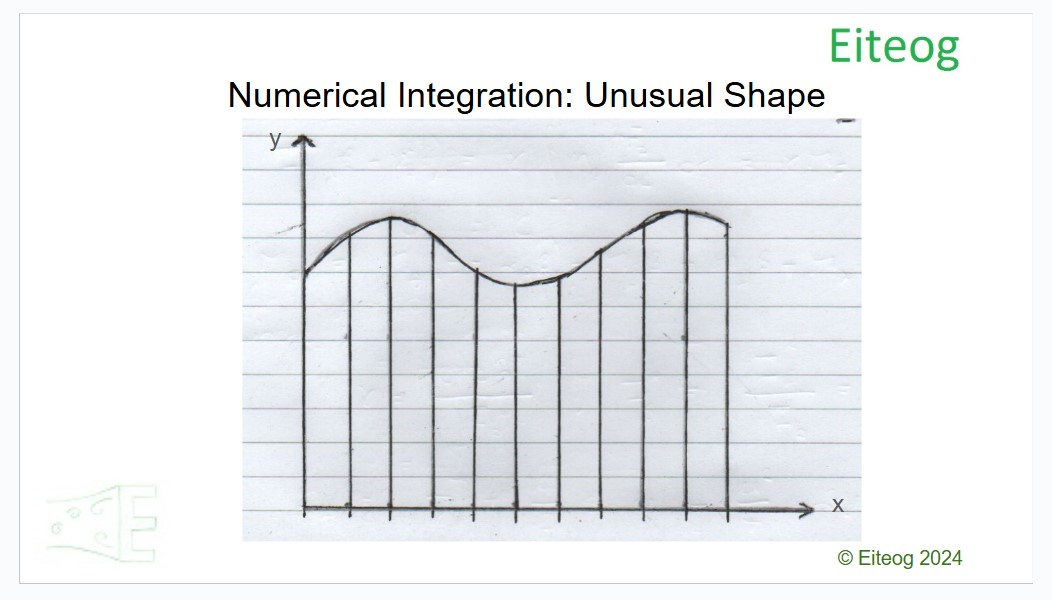
Unusually shaped area split into strips for numerical integation

This may be familiar to you and you may have done it before without knowing your were using numerical integration! Obvious there is error as the strips are not exactly rectangulars so the more strips you use the smaller the error as smaller strips are closer in shape to a rectangular.

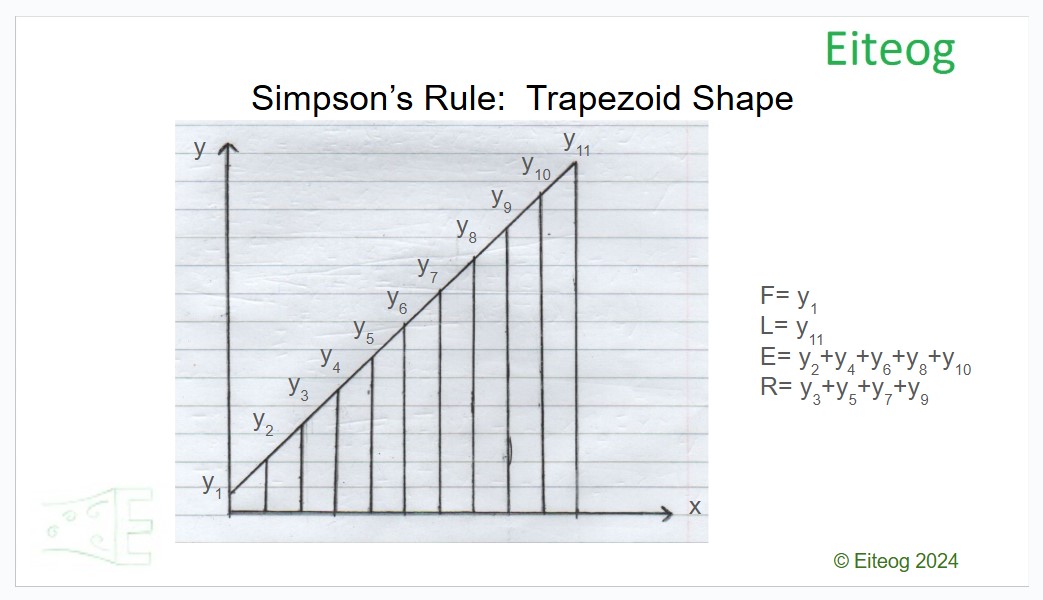
Another way to reduce the error is to use Simpson's rule which rather than calculating the area directly being adding all the small approximate rectangular areas together you use an equation to do it. The equation accounts for the fact that you are using approximate rectrianglar areas and gives a better estimate of the area by assuming they are trapezoid in shape rather rectrianglar. The equation is as follows:

\[A=\frac{s}{3} \left[ \left( F+L_s \right)+4E+2R \right] \]

Where s is the width of each of even width strips, F is the height of the first ordinate, L_s is the height of the last ordinate, E is the sum of the heights of all the even position ordinates and R is the sum of the heights of the remaining ordinates. The picture below hopefully should illustrate which ordinates are F, L_s and which should be included in E and R:

Trapezoid shape labelled to explain Simpsons rule, F, Ls, E and R

We also going to look at example using the area that was used in the original article on integration [1], so hopefully this will clear up any misunderstandings about Simpsons rule. This area is simple and in reality you do not need to use numerical integration but it is good for demonstrating how useful numerical integration is.

From the original article [1] on integration the area for trapezoid is as follows:

\[A = \frac{1}{2} (a + b) L \]

In that article we also assumed the trapezoid had two sides, a=2, b=30 and a length, L=4 which gives an area below:

\[A = \frac{1}{2} (2 + 30) 4 = 64 \]

In order to use integration we must assume the top bounding the the area between the 'y' and the 'x' axis is that of linear equation [3]:

\[y = mx + c \]

Now to work out 'm' and 'c', we can use the same method used to solve simultaneous equations [4], but it is actually simpler than that. We know that when x=0, y=a and when x=L, y=b, therefore, c=a and m=(b-a)/L. Therefore our linear equation will have c=2 and m=7:

\[y = 7x + 2 \]

If we choose to split the shape into ten stripes then we will have 11 points to plot with each strip being 0.4(4/10) in width.

Point Description	X ordinate	Y ordinate	Approximate Strip Area
1-First	0	2	0
2-Even	0.4	4.8	4.8x0.4=1.92
3-Remain	0.8	7.6	7.6x0.4=3.04
4-Even	1.2	10.4	10.4x0.4=4.16
5-Remain	1.6	13.2	13.2x0.4=5.28
6-Even	2.0	16	16x0.4=6.4
7-Remain	2.4	18.8	18.8x0.4=7.52
8-Even	2.8	21.6	21.6x0.4=8.64
9-Remain	3.2	24.4	24.4x0.4=9.76
10-Even	3.6	27.2	27.2x0.4=10.88
11-Last	4	30	30x0.4=12

If you add up all the approximate strip areas you get:

\[1.92+3.04+4.16+5.28+6.4+...+\] \[+...+7.52+8.64+9.76+10.88+12\] \[=69.6\]

Using Simpson rule, s=0.4, F=2, L_s=30 and E is:

\[E=4.8+10.4+16+21.6+27.2=80 \]

With R

: \[R= 7.6+13.2+18.8+24.4=64\]

The area calculated by Simpsons is given below:

\[A=\frac{s}{3} \left[ \left( 2+30 \right)+4\left(80\right)+2\left(64\right) \right] \] \[A=64\]

Comparing the two area calculations you can see that the method using Simpson's rule gives the exact correct answer just using 10 strips. More complicated shapes may need more strips to give as accurate an answer. However, I would suggest trying it with more strips say increasing from 10 to 100, if you use a spreadsheet such Google sheets or MS Excel you could use up to 1000, and you should see the accuracy of the estimate increase, probably 100 strips would you give very close to 64 without using Simpson's rule. How accurate you need the answer all depends on what you are using it for. For further reading on integration see references [5] and [6].

Please leave a comment on my facebook page or via email and let me know if you found this blog article useful and if you would like to see more on this topic. Most of my blog articles are on:

Mathematics
Helicopters
VTOL UAVs (RC Helicopters)
Sailboat Design and Boatbuilding

If there is one or more of these topics that you are specifically interested in please also let me know in your comments this will help me to write blog articles that are more helpful.

References:

[1] http://www.eiteog.com/EiteogBLOG/No50EiteogBlogIntegration.html

[2] http://www.eiteog.com/EiteogBLOG/No48EiteogBlogDifferentiation.html

[3] http://www.eiteog.com/EiteogBLOG/No15EiteogBlogLinear.html

[4] http://www.eiteog.com/EiteogBLOG/No40EiteogBlogSimEquations.html

[5] Engineering Mathematics, K. A. Stroud, Fourth Edition, 1995, Macmillan

[6] Further Engineering Mathematics, K. A. Stroud, Fourth Edition, 1996, Palgrave Macmillan

Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.