\[ \]

Vectors and Scalars

Issue No 45, 25 September 2023

By: Anthony O. Ives

A vector quantity is a quantity that has both magnitude and direction such as velocity. Velocity should be described with a direction for example when descriding wind conditions you usually say something like '10 knots north easterly'. A scalar quantity is a quantity that has no direction or none specified such a mass, volume, density, temperature, etc. While velocity is considered a vector, speed can be considered a scalar hence velocity can be defined as speed with direction. Examples of other vector properties are forces, distances even torque and moments can have direction but just not as obvious, so technically torque and moment can be specified as vectors.

Torque and moment direction is usually considered perpendicular to its rotation direction, similar can be assumed for angular velocity, RPM, etc. Vector properties can be defined as a magnitude and its direction defined as angle to some reference plane, for three dimensional vectors a second angle would be needed to a plane perpendicular to reference place of the first angle. This article is mainly going to consider two dimensional vectors for simplicity.

Vectors can also be defined in i,j notation for two dimensional vectors and i,j,k for three dimensional vectors. We will discuss how to go from i,j notation to magintude and angle but first I want to discuss how trignometry [1],[2] is used to analyse vectors and also how vectors are important and useful. However, i,j and i,j,k vector notation would look something like this:

\[V = ai+bj\] \[V = ai+bj+ck\]

Where V is the vector property, a is the magnitude of the vector in the x or horizontal direction, b is the magnitude of the vector in the y or vertical direction, c is the magnitude of the vector in the z direction for three dimensional vectors which is both pendicular to the x and y directions.

In order to see the usefullness of the vectors I going to describe a simple example where a mass in the shape of a ball is suspended from a ceiling using two strings at different angles to the ceiling one at 60 degrees and the other at 30 degrees. You can use vector theory to determine the tension in the strings, below gives a diagram of the scenario:

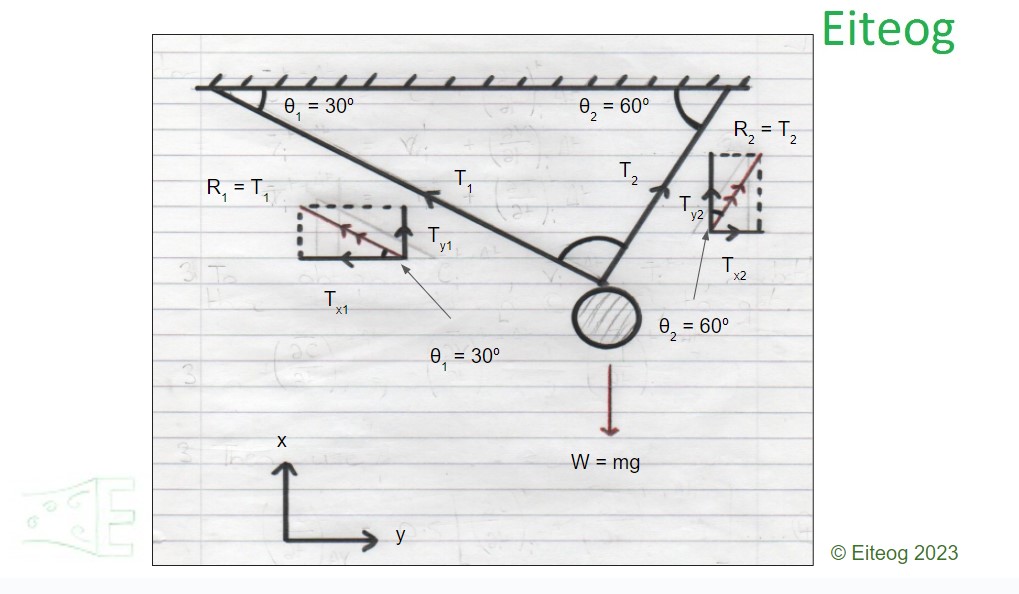
Simple Vector Diagram

Trignometry and pythargoras theorem is used in the same way as you would to work out geometry only instead of just a length or distance you can use any vector properties in this case we will be looking at forces. You can actually use scale drawings to work out vectors directions and magnitudes in same way as you would also work out an unknown length or angle. In the case of scale drawings a 1 centmetre for example could represent 1 newton or 1 knot, etc depending on the vector property you are trying to determine. Scale drawings can be still used in sailboat navigation we will look at them in more detail in later articles. For now we are going to use trignometry to determine the tension in the string, we assume the ball has a mass of 5 kilogrammes and gravity is 9.81 metres per second squared. We resolve the forces in both the vertical and horizontal directions:

Horizontal: \[T_1 sin \theta_1 + T_2 sin \theta_2 = mg\]

Vertical: \[T_1 cos \theta_1 + T_2 cos \theta_2 = 0\]

You now have two equations and two unknowns hence you should be able recognise these as simultaneous equations from the earlier article on simultaneous equations [3]. Assuming m = 5 kg, θ₁ = 30 deg and θ₂ = 60 deg you should be able to determine T₁ and T₂ as follows:

Horizontal: \[T_1 sin 30 + T_2 sin 60 = 5 \times 9.81\]

Vertical: \[T_1 cos 30 = T_2 cos 60\]

Vertical: \[T_1 cos 30 - T_2 cos 60 = 0\]

\[T_1 = T_2 \frac{cos 60}{cos30} = 0.57735 T_2\]

\[0.57735 T_2 sin 30 + T_2 sin 60 = 5 \times 9.81\]

\[T_2 (0.57735 sin 30 + sin 60) = 5 \times 9.81\]

\[T_2 = \frac{5 \times 9.81}{0.57735 sin 30 + sin 60} = 42.48 N\]

\[T_1 = 0.57735 T_2 = 0.57735 \times 42.48 = 24.53 N\]

The tensions calculated in the strings are as you would expect, the string that is more vertical is taking more of the weight whereas the string that is more horizontal is taking less of the weight.

The notation of i,j can be worked in a similar way where:

\[V = V_{mag} cos \theta i + V_{mag} sin \theta j\]

So you could workout the string tensions using the i,j notation by noting the three forces as follows:

\[T_{v1} = T_1 cos 30 i + T_1 sin 30 j\]

\[T_{v2} = -T_2 cos 60 i + T_2 sin 60 j\]

For the i term T₂ is negative to note that its horizontal component is in the opposite direction from the T₁ horizontal component.

\[W_v = mg cos 90 i + mg sin 90 j = 0 i + mg j\]

You can then add the vectors together as below:

\[W_v = T_{v1} + T_{v2}\]

So you can just add the i terms together and then add the j terms together, and you can then again deduce the simultaneous equations as before. Magnitude and angle of direction for two dimensional vectors can be determined as follows:

\[V = ai+bj\]

\[\begin{vmatrix} V \end{vmatrix}= \sqrt{a^2+b^2}\]

\[\theta = tan \frac{b}{a}\]

This principle can be easily extended to three dimensional vectors as can be done for pythargoras theorem in determining three dimensional distances [3]. Further information can be found on vectors in the Stroud engineering maths textbooks [4], [5] as well as how matrices can be used in vector manipulation, etc.

Please leave a comment on my facebook page or via email and let me know if you found this blog article useful and if you would like to see more on this topic. Most of my blog articles are on:

Mathematics
Helicopters
Woodworking and Boatbuilding

If there is one or more of these topics that you are specifically interested in please also let me know in your comments this will help me to write blog articles that are more helpful.

References:

[1] http://www.eiteog.com/EiteogBLOG/No12EiteogBlogTrig.html

[2] http://www.eiteog.com/EiteogBLOG/No22EiteogBlogPythargoras.html

[3] http://www.eiteog.com/EiteogBLOG/No40EiteogBlogSimEquations.html

[4] Engineering Mathematics, K. A. Stroud, Fourth Edition, 1995, Macmillan

[5] Further Engineering Mathematics, K. A. Stroud, Fourth Edition, 1996, Palgrave Macmillan

Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.