
\[ \]
\[ \]
\[ \]
Issue No 12, 28 November 2022
By: Anthony O. Ives
Trigonometry has many applications in engineering, architecture, carpentry and joinery. Trigonometry can be used to determine angles, distances, components of velocities, forces and other vector properties. The trigonometry equations apply to right angle triangles essentially one of the three angles must be 90 degrees however, most triangles that do not have a right angle can usually be split into 2 or more right angle triangles.
The trigonometry equations are given below:
\[sin \theta = \frac{y(opposite)}{R(hypotenuse)} \]
\[cos \theta = \frac{x(adjacent)}{R(hypotenuse)} \]
\[tan \theta = \frac{y(opposite)}{x(adjacent)} \]
Below gives a diagram explaining the trigonometry notation, it also shows the relationship between cartesian coordinates (x, y) and polar coordinates (R, θ).
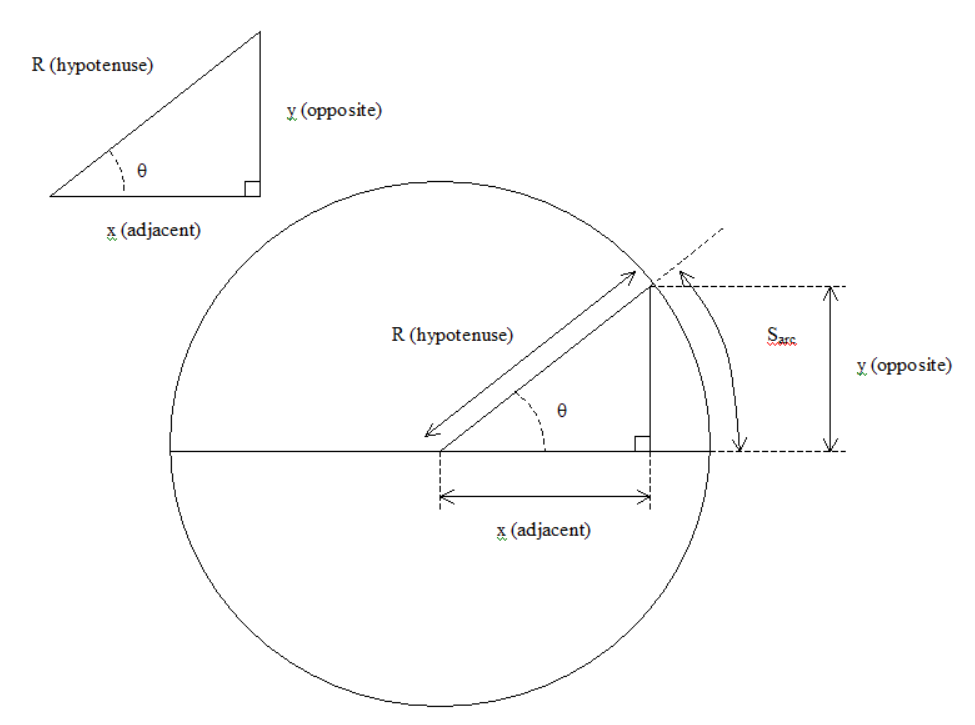
Reference has be made to cartesian and polar coordinates in the previous paragraph, so we will explain what they are. If you want to give a position for example on map from a specific point you would need to give two distances from a reference point if you want to know the position in 2D (2 Dimesional). One distance is in horizontal direction, x and the other in the vertical direction, y. If you give your position in 3D (3 Dimensional) then need to give an additional distance, z this would go into or out of the map plane. Using 2 distances (if considering 2 Dimesions only) on axis that are at right angles to each other is essentially cartesian coordinates. Polar coordinates use a distance, R and an angle, θ for 2 dimensional cases this typically looks like what you would see on a radar scope. In three dimensional cases polar coordinates would use a second angle, φ coming out of or into the radar scope. Trigonometry equations can be used to convert polar coordinates into cartesian coordinates and vice versa in both 2D and 3D. The 2D cases however are easier to visualise as in the diagram given in this article but trigonometry is also used in 3D cases, we will discuss this in a future article looking at pythagoras theorem.
We can use an approximation for small angles which simples the trigonometry equations. These approximate expressions can be used with more reasonable accuracy for angles up to 25 degrees. So for small angles you can assume that R is roughly equal to x, and Sarc is roughly equal to y. It then follows from the geometry relationships we defined in Ref [1] that:
If R ≈ x, Sarc ≈ y and if θ is in radians and not degrees then:
\[ \theta_{radians} \approx \frac{S_{arc}}{R} \approx \frac{y}{x} \approx tan \theta \]
\[ \theta_{radians} \approx \frac{S_{arc}}{R} \approx \frac{y}{R} \approx sin \theta \]
\[ \frac{x}{R} \approx 1 \approx cos \theta \]
Therefore:
\[ \theta_{radians} \approx tan \theta \approx sin \theta\]
\[cos \theta \approx 1 \]
Also make sure your calculator is setup to take the correct angle units, radians or degrees for the trigonometry functions if you are using it to confirm these approximations. Typical calculator trigonometry functions is given in the diagram below:

The buttons in the above picture converts an angle to a dimension ratio for the relevant trigonometry function. The inverse of the function converts the ratio back to an angle it is usually accessed using the same buttons but in combination with a shift button. You can usually change your calculator settings so the trigonometry functions can take degrees. radians, etc. Most calculators usually have degrees set up by default, there is usually some indication on the screen either a 'd' or 'deg' for degrees or 'r' or 'rad' for radians. The angle indication is usually along the top of the screen in small text. A good way of verfying that the calculator is the correct angle mode is checking sin of 90 degrees gives you 1 and cos of 90 degrees gives 0. The picture below shows how the angle indication typically appears on a calculator screen:

The 1 in 60 rule or 1/60 rule is commonly used by pilots to do mental arithmetic in the cockpit to determine a heading correction when they find they have been blown off course slightly. This is usually due to their predicted wind not being the same as their actual wind. In reality it is just a slightly further simplification of the expression which assumes π ≈ 3. In Ref [1] we explained how to convert angles from degrees to radians. Using this you can simplfy the trigonometry expressions further for small angles:
\[\theta_{degrees} = \frac{180}{\pi} \theta_{radians} \approx 60 \theta_{radians}\]
\[\theta_{degrees} \approx 60 \frac{y} {x} \approx 60 \frac{y}{R} \]
In case you did not already know the sum of the angles in a triangle equals 180 degrees hence for right angle triangles the two remaining angles must total 90 degrees. So if you always use the smallest angle it will never exceed 45 degrees. Hence if you are finding you a getting big angle greater than 45 degrees reorientate the triangle to use the approximate expressions, essentially change what you are using for x(adjacent) and y(opposite) around. R(hypotenuse) is fixed by where the right angle is. While the expressions are less accurate above angles of 25 degrees for certain applications the accuracy may be exceptable up to angles of 45 degrees. You also make an assumption that for angles approaching 45 degrees, for example between 40 and 50 that x(adjacent) ≈ y(opposite). For applications like dead reckoning navigation whether for aviation, sailing or trekking its ok to use angles up to 45 degrees. I generally use the simplfied expressions for dead reckoning navigation. For carpentry, joinery or similar projects its depends on the accuracy of the measuring instrument you are using, however I always the full trigonometry expressions for these types of projects. Just as a note the simplfied expressions are less accurate for tan(θ) than they are for sin(θ).
Remembering trigonometry equations can be done by using a memory aid or mnemonic. I always preferred to remember things by understanding them, I never learned my times tables I just work them out when I need them. In a way the simplfied trigonometry expressions helps you understand the relationship between the angles and length of the sides of a triangle. Generally understanding something helps you remember it clearly forever while learning a rhythm generally the understanding can fade with time.
I hope you found this article useful and it cleared up any misunderstanding you have of trigonometry.
Please leave a comment on my facebook page or via email and let me know if you understand how circle geometry and trigonometry is related. Also please let me know if you think trigonometry will be useful in carpentry, woodworking or other DIY projects you are working on.
References:
[1] http://www.eiteog.com/EiteogBLOG/No10EiteogBlogCircle.html
Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.
For any inquires contact: [email protected] copyright © Eiteog 2022