
\[ \]
\[ \]
\[ \]
Issue No 37, 31 July 2023
By: Anthony O. Ives
Quadratic equations were introduced previously [1] as a 2nd order polynomial equation. So a polynomial equation is a general term used to describe equations such as cubic, quartic equations, etc where a cubic equation is a 3rd order polynomial and a quartic equation is a 4th order polynomial. A polynomial can be of any order from 1 to infinity such as where the order denotes the highest index term. Generally the higher the order of the polynomial the better it is at curve fitting.
In mathematics curve fitting is where you have series of points such as data from experiment or certain geometric shape such as an airfoil and you want to find an equation that can be used calculate the position of those points. Commonly a linear equation [2] is used which is techincally a 1st order polynomial however, if the points do not appear to be following an exact straight line you may need to use a polynomial, the more complex the shape the higher the order of the polynomial you will need to use.
Curve fitting is only one of the many uses that polynomials have, they can also useful for analysing flight dynamics and control systems. Polynomial can been expanded in a similar way as quadratic equation for example multiplying a quadratic equation by a linear equation will give a cubic equation as below:
\[y = (x + 9)(x + 4)(x + 3) \]
\[= (x + 9) (x^2 + 7x + 12) \]
\[= x (x^2 + 7x + 12) + 9 (x^2 + 7x + 12) \]
\[= x^3 + 7x^2 + 12x + 9x^2 + 7(9)x + (9)12) \]
\[= x^3 + (7+9)x^2 + (12 + (7)9)x + (9)12) \]
\[= x^3 + 16x^2 + 75x + 108 \]
The expansion of the cubic equation is a similar to how a quadratic equation is expanded as seen below.

However, with a cubic equation you have an extra term to consider compared with the quadratic equation. If you multiply a cubic equation by another linear equation you will get a quartic equation as in example below:
\[y = (x + 2)(x + 9)(x + 4)(x + 3)\]
\[ = (x + 2) (x^3 + 16x^2 + 75x + 108) \]
\[= x(x^3 + 16x^2 + 75x + 108) + 2(x^3 + 16x^2 + 75x + 108) \]
\[= x^4 + 16x^3 + 75x^2 + 108x + 2x^3 + 32x^2 + 150x + 216) \]
\[= x^4 + (16+2)x^3 + (75+32)x^2 + (108+ 150)x + 216) \]
\[= x^4 + 18x^3 + 107x^2 + 258x + 216 \]
The quartic equation can also be expanded as two quadratic equations, by first expanding the two linear equations as below:
\[(x + 2)(x + 9) = x^2 + 11x + 18 \]
\[y = (x + 2)(x + 9)(x + 4)(x + 3) \]
\[= (x^2 + 11x + 18) (x^2 + 7x + 12) \]
\[= x^2(x^2 + 7x + 12) + 11x(x^2 + 7x + 12) + 18(x^2 + 7x + 12) \]
\[= x^4 + 7x^3 + 12x^2 + 11x^3 + 77x^2 + 132x + 18x^2 + 126x + 216) \]
\[= x^4 + 18x^3 + 107x^2 + 258x + 216) \]
However, while there are many ways to expand a ploynomial probably the most straight forward is as in the diagram below:
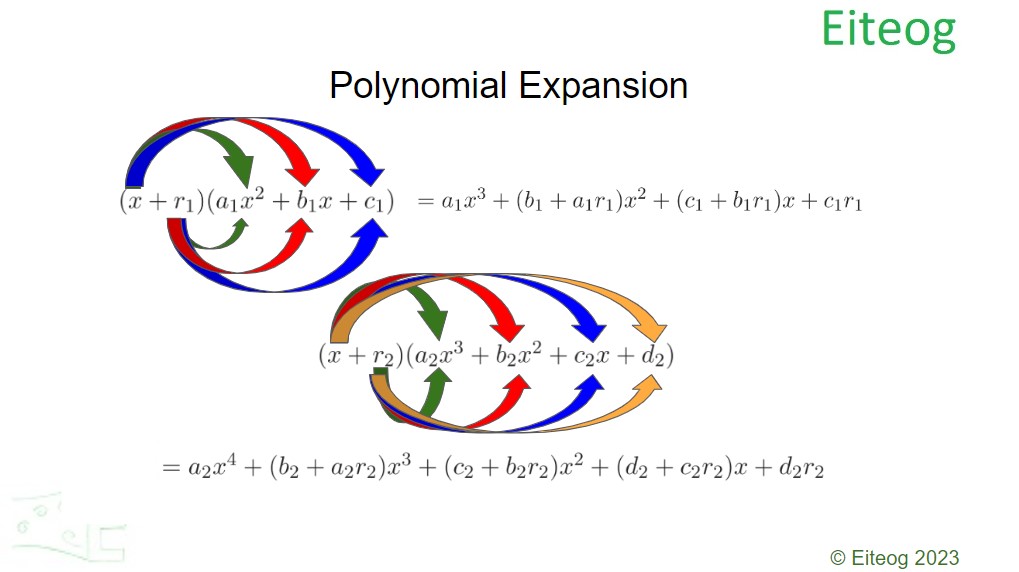
An important principle to note is that a quartic can consist of two quadratic equations which means a quartic can have four complex roots [1] where as a cubic equation can consist of only one quadratic equation hence can have only one set of complex roots. Likewise a 6th order polynomial have 6 complex roots, of 8th order polynomial have 8 complex roots, etc. However, a 5th order, 7th order, 9th order polynomials must all have a least one real root even if the remaining roots are complex. Therefore a polynominal with an order that is an odd number must have at least one real root, this is important concept to remember for flight dynamics. Generally the complex roots are represented by their quadratic equations in a factorised polynomial as in the example below:
\[x^2 + 8x + 25 = (x + (4-3j))(x + (4+3j))\]
\[y = (x + 2)(x + 9)(x^2 + 8x + 25)\]
\[= x^4 + 19x^3 + 131x^2 + 419x + 450) \]
Apart from the quadratic equation most other higher order polynomials have to have their roots determined by numerical methods and long division. If the polynomial has more than one set of complex roots the numerical scheme can become complex. A future article will discuss determining the roots of higher polynomial equations.
A polynomial can be represented by the following expression if has a set of identical roots:
\[y = (x + a)^n \]
An example is given below that uses a quartic equation again:
\[y = (x + 4)^4 \]
\[= (x + 4)(x + 4)(x + 4)(x + 4) \]
\[= (x + 4)(x + 4)(x^2 + 8x + 16) \]
\[= (x + 4)(x^3 + 36x^2 + 48x + 64) \]
\[= x^4 + 40x^3 + 192x^2 + 256x + 256 \]
The graph below shows what the various plots for the polynomial examples given, the curve for a cubic equation will cross the y-axis 3 times, a quartic equation will cross the y-axis 4 times however, a quartic equation with one set of complex roots will only cross the y axis 2 times if it had two sets of complex roots it would not cross the y-axis at any point.
Further information on polynomials can be found in Reference [3] and [4], there will further articles on what polynomials can be used for and how they can be solved.
Please leave a comment on my facebook page or via email and let me know if you found this blog article useful and if you would like to see more on this topic. Most of my blog articles are on:
Mathematics
Helicopters
VTOL UAVs (RC Helicopters)
Sailing and Sailboat Design
If there is one or more of these topics that you are specifically interested in please also let me know in your comments this will help me to write blog articles that are more helpful.
References:
[1] http://www.eiteog.com/EiteogBLOG/No34EiteogBlogQuadratic.html
[2] http://www.eiteog.com/EiteogBLOG/No15EiteogBlogLinear.html
[3] Engineering Mathematics, K. A. Stroud, Fourth Edition, 1995, Macmillan
[4] Further Engineering Mathematics, K. A. Stroud, Fourth Edition, 1996, Palgrave Macmillan
Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.
For any inquires contact: [email protected] copyright © Eiteog 2023