\[ \]

Pythargoras Theorem

Issue No 22, 3 April 2023

By: Anthony O. Ives

Pythargoras theorem enables you to determine the length of the remaining side of a right angle triangle if you already know the length of the other two sides. Pythargoras theorem is an important theorem of trigonometry [1]. Like trigonometry it is important for a wide range of applications including engineering, vector analysis, navigation, architecture, etc. The distance formula for cartesian co-ordinates is also derived from pythargoras theorem. The distance is used in a wide range of applications including navigation and is very important for modern satelite navigation systems such as GPS Navstar [2].

The equation for pythargoras theorem is given below:

\[R = \sqrt{x^2 + y^2}\]

Where R is the length of hypotenuse side of the triangle, x is the length of adjacent side of the triangle and y is the length of the opposite side of the triangle. The hypotenuse, adjacent and opposite sides of a triangle as well x, y and R are graphically defined in the diagram below:

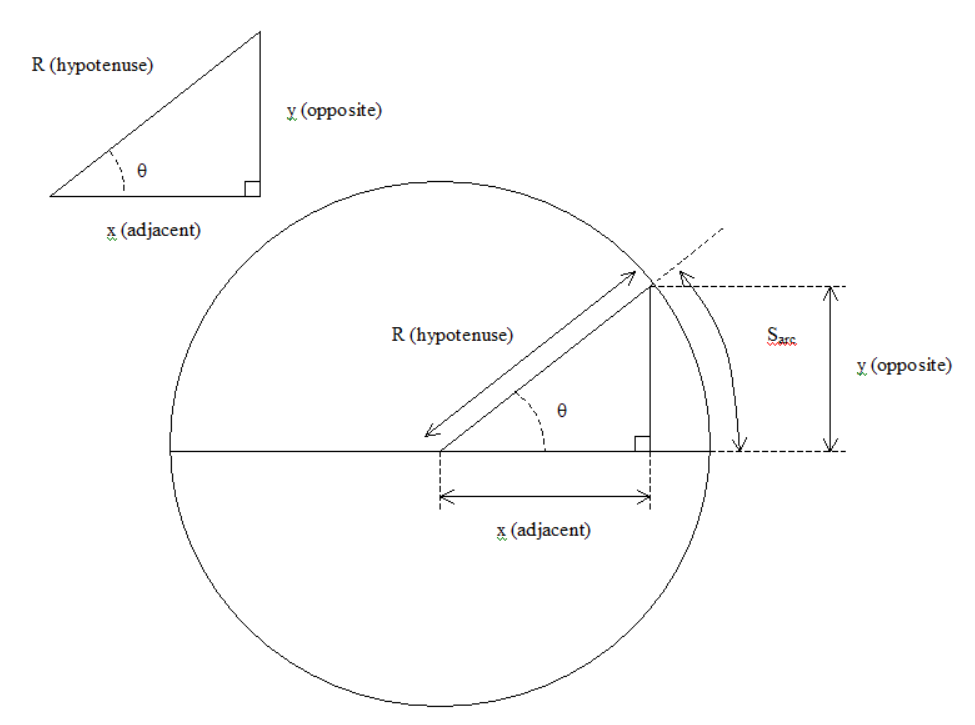
Trigonometry Diagram

The pythargoras equation can be manipulated so that say 'y' can be determined from 'R' and 'x' or 'x' can be determined from 'R' and 'y'. The two equations for 'x' and 'y' are given below:

\[x = \sqrt{R^2 - y^2}\]

\[y = \sqrt{R^2 - x^2}\]

Pythargoras theorem can be used to derive an equation that is used to determine the distance between two points [3] in space as in the diagram below:

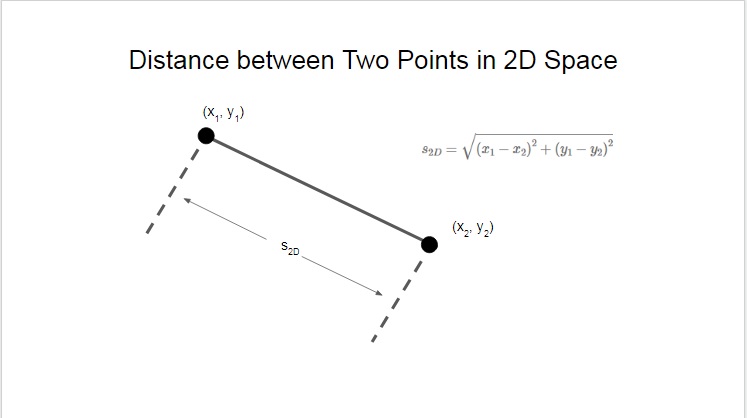
Distance between Two Points in a 2D Space

The equation for determining the distance between to two points in a 2D space are given below:

\[s_{2D} = \sqrt{ \left( x_1 - x_2 \right)^2 + \left( y_1 - y_2 \right)^2}\]

Where s_2D is the distance between the two points in a 2D space, x₁ is the x coordinate of the first point, x₂ is the x coordinate of the second point, y₁ is the y coordinate of the first point and y₂ is the y coordinate of the second point.

The equation for distance can be extended to a 3D space and would look like the following for a 3D space:

\[s_{3D} = \sqrt{ \left( x_1 - x_2 \right)^2 + \left( y_1 - y_2 \right)^2 + \left( z_1 - z_2 \right)^2}\]

Where s_3D is the distance between the two points in a 3D space, z₁ is the z coordinate of the first point, z₂ is the z coordinate of the second point.

Global Navigation Satelite Systems (GNSS) use a ground receiver which recieves the distance between the receiver and a number of satelites. The position of each of the satelites is known and transmitted to the reciever using this information it can be seen that you could calculate your position using the distance equation. Essentially you want to find out your own positon which is your x, y, z coordinates that is three unknowns. You know the distance from your position to each satelite giving you three distances as well as the x, y, z coordinates for each satelite. Using this information you can setup three equations with three unknowns and with a bit of complex simulateous equation manipulation you can determine your x, y, z coordinates and hence your position. This is simplfied version of the procedure that Global Navigation Satelite Systems (GNSS) use however actual Global Navigation Satelite Systems (GNSS) use more a complex calculation method and require a minimum of 4 satelites to determine your position [2] where as you may have noticed the simplfied procedure requires only three satelites. The fourth satelite is required to calcuate a time which is mainly to do with accuracy just using three satelites would in reality produce large errors in the position calculation.

Please leave a comment on my facebook page or via email and let me know if you found this blog article useful and if you would like to see more on this topic. Most of my blog articles are on:

Mathematics
Helicopters
VTOL UAVs (RC Helicopters)
Sailing and Sailboat Design

If there is one or more of these topics that you are specifically interested in please also let me know in your comments this will help me to write blog articles that are more helpful.

References:

[1] http://www.eiteog.com/EiteogBLOG/No12EiteogBlogTrig.html

[2] Instrumental Flying Handbook, FAA-H-8083-15B, 2012, United States Department of Transportation, Federal Aviation Administration, https://www.faa.gov/sites/faa.gov/files/regulations_policies/handbooks_manuals/aviation/FAA-H-8083-15B.pdf

[3] Engineering Mathematics, K.A. Stroud, Fourth Edition, 1995, Macmillan

Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.