\[ \]

Helicopter Hover and Propeller Power Coefficent and Efficiency

Issue No 16, 30 January 2023

By: Anthony O. Ives

In order to determine power required to turn a helicopter rotor a power coefficient can be calculated which is similar to thrust coefficient see Ref [2]. The power required for a helicopter rotor is closely related to drag in the form of the drag polar equation as seen in Ref [1]. Propellers and helicopter rotors are very similar and generally use the same equations to calculate thrust and power. Efficiency is the amount of power that is usefully converted to thrust. Efficiency for propellers is propulsion efficiency, for helicopter rotors its hover efficiency. Both propulsion and hover efficiency are calculated slightly differently.

Power is defined by power coefficient in a similar way that thrust is defined by thrust coefficient as Ref [2], the only difference is tip velocity, R ω is cubed instead squared. The symbols are defined as they are Ref [2]. R is Rotor radius, ω is rotor angular velocity, ρ is air density, P is power and C_P is power coefficient. The equation below defines P in terms of power coefficient.

P=ρ (π R²) (R ω)³ C_P

Power coefficient can then be calculated from thrust coefficient C_P, inflow ratio λ and rotor airfoil zero lift drag coefficient C_D0 as well as solidary ratio σ and a tip loss factor K_TL. The equation is given below:

\[C_P = K_{TL} \lambda C_{T} + \frac{\sigma C_{D0} }{8} \]

The tip loss factor, K_TL is typically 1.15, zero lift drag coefficient, C_D0 is typically 0.01. λ the inflow ratio is described in more detail in Ref [3]. This power coefficient equation is related to the drag polar, one part represents induced power loss depending on the thrust produced while the other part represents power loss even if no thrust is produced. The thrust a rotor produces is directly related to the lift it produces as seen Ref [2]. The equation for rotor power loss is in a different form from the drag polar equation due to complications of rotary wing aerodynamics but how power is lost is due to the same loss processes.

Ref [4] briefly introduced propulsion efficiency and using the equations defined in this article, Ref [2] and [3] you can calculate propulsion efficiency for certain flight conditions. Propulsion efficiency is defined with respect to flight velocity with regard to fixed wing aircraft for a helicopter this is the same as climb rate. See equation below which shows how efficiency is related to thrust and power coefficients:

\[\eta =\frac{TV} {P} =\frac{\rho (\pi R^2) (R \omega)^2 C_T V} {\rho (\pi R^2) (R \omega)^3 C_P} \]

\[\eta =\frac{TV} {P} =\frac{C_T V} { R \omega C_P} =\frac{C_T \lambda_C} {C_P} \]

Therefore: \[\lambda_C =\frac{ V} { R \omega } \]

λ_C is climb inflow for helicopters but advance ratio for fixed wing propeller driven aircraft. Advance ratio for helicopters is defined differently as this is due to it moving forward and not upward so air comes at angle through rotor for a helicopter. A specific future article will discuss helicopter forward flight and advance ratio in more detail but Ref [5] gives an in depth mathematical explanation of helicopter forward flight as well as what has been discussed in this article.

Using the equations that have been introduced you could plot a graph of propulsion efficiency versus advance (climb for helicopters) ratio for fixed pitched propellers. The graph would demonstrate that fixed pitched propellers give a maximum efficiency for one particular speed or advance ratio. Efficiency decreases as speed reduces below or increases above this specific speed or advance ratio. Therefore why variable pitch propellers are more efficient for various flight speeds as they can be adjusted to a pitch that is most efficient for the specific speed the aircraft is travelling at. The below graph gives a typical graph of propulsion efficiency against advance ratio for a propeller.

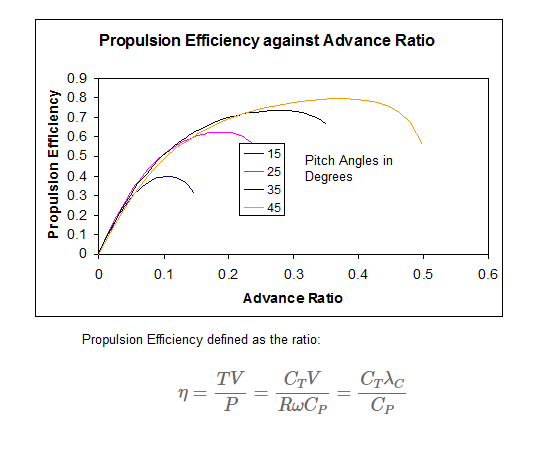
Propeller Propulsion Efficiency

Helicopters are usually designed to be as efficient as possible in hover. The reason for this is a helicopter requires the most power in hover than in any other phase of flight. Therefore it is useful to determine a hover efficiency. Hover efficiency is defined in a similar way to propulsion efficiency for propeller the only difference is you cannot use the climb ratio as in hover the helicopter is not climbing and is in theory stationary. The hover efficiency uses hover inflow ratio which was defined in Ref [3]. The hover efficiency can then be calculated using the following:

\[\eta_h =\frac{C_T \lambda_h} {C_P} \]

Hover efficiency is usually used to find the almost efficient rotor pitch angle but can used to determine the best combination of rotor solidary ratio, rotor pitch angle or rotor area, etc. Power required in helicopter forward flight is lower than in hover. The pilot has to reduce power to avoid climbing when he transitions to forward flight. The speed which a helicopter requires the least power is called the translational lift speed it also known as the best rate of climb speed. However, future articles will look at helicopter forward flight in more detail, but I hope this article has helped you understand rotor power as well as the difference between propulsion and hover efficiency and how it ties in rotor thrust and inflow introduced in Ref [2] and [3].

Please leave a comment on my facebook page or via email and let me know if you found this blog article useful and if you would like to see more on this topic. Most of my blog articles are on:

Mathematics
Helicopters
Woodworking and Boatbuilding

If there is one or more of these topics that you are specifically interested in please also let me know in your comments this will help me to write blog articles that are more helpful.

References:

[1] http://www.eiteog.com/EiteogBLOG/No2EiteogBlogDragCD.html

[2] http://www.eiteog.com/EiteogBLOG/No4EiteogBlogThrust.html

[3] http://www.eiteog.com/EiteogBLOG/No11EiteogBlogThrust.html

[4] http://www.eiteog.com/EiteogBLOG/No6EiteogBlogRange.html

[5] Helicopter Theory, Wayne Johnson, 1980, Dover Publications

Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.