\[ \]

Airspeed Airspeed

Issue No 66, 31 March 2025

By: Anthony O. Ives

Airspeed can be defined in different ways such as True Airspeed (TAS), Calibrated or Rectified Airspeed (CAS/RAS), Equivalent Airspeed (EAS), Indicated Airspeed (IAS) and Mach number. This article aims to describe the relationship between each of the airspeeds and how to convert between them using equations or a mechanical flight computer such as the CPR-5.

True Airspeed (TAS) is probably simplest to explain as it is the actual speed the aircraft is moving relevant to the air. Therefore the aircraft does not have to be moving to have an airspeed if there is a wind so therefore wind speed (WS) has to be added or subtracted from the ground speed in order to get true airspeed. Wind speed is positive for a headwind and negative for a tail wind. Ground speed (GS) is the speed which the aircraft moves relevant to the ground hence:

TAS = GS + WS

Indicated Airspeed (IAS) is the airspeed displayed on the airspeed indicator. Indicated Airspeed is essentially calibrated airspeed with some errors (hopefully small errors) due to mechanical defects and position error. Position error is due aerodynamic effects distorting pressure measurement around the pitot probe. The Pitot probe determines airspeed from total and static pressure, but is calibrated at sea level conditions hence why is does not give true airspeed directly.

Mach number, M is the next airspeed that needs to be defined as its allows you to decide whether or not you need to consider compressibility. Mach number is simply the true airspeed divided by the local speed of sound, hence for a Mach number of 1 the true airspeed will be equal to the speed of sound. For Mach number above 0.3 or 0.4 you need to consider compressibility and will have an effect on what airspeed your airspeed indicator is measuring. Some aircraft (usually high speed aircraft that fly at speeds above Mach number of 0.7 close to the speed of sound) have a separate indicator for measuring Mach number. Mach number can be calculated from true airspeed (TAS) and the speed of sound (a) as follows:

\[ M =\frac{TAS}{a} \]

The speed of sound is calculated using the local air temperature (T), the Gas Constant (R=287JK^-1kg^-1) and the ratio of heat capacities (γ=1.4) as below:

\[a = \sqrt{\gamma RT} \]

Equivalent Airspeed (EAS) ρ₀ is the airspeed (without errors) given by the airspeed indicator for low speed flight below a Mach number of 0.3/0.4 and due to the airspeed indicator being calibrated at sea level. The equivalent airspeed can be calculated using the sea level air density, 1.2256kgm^-3 and the air density at the altitude the aircraft is being flown at using the following equation:

\[ EAS=TAS \sqrt{\frac{\rho}{\rho_0}} \]

Calibrated or Rectified Airspeed (CAS/RAS) is the airspeed (again without errors) given by the airspeed indicator for nearly all flight speeds however, as the aircraft approaches the speed of sound strange things meant happen due to shock wave formation, etc. For Mach numbers up to approximately 0.8 the airspeed indicator is giving calibrated airspeed. For speeds below Mach number of 0.3/0.4 the airspeed indicator gives both calibrated and equivalent airspeed as at low speed both calibrated and equivalent airspeed are nearly equal. Calibrated airspeed is same as rectified airspeed, 'calibrated airspeed (CAS)' is the British term were as 'recfified airspeed (RAS)' is the American term. Calibrated airspeed can be calculated using the following equation:

\[ CAS=EAS \left[ 1+ \frac{1}{8}\left( 1-\delta \right) M^2 +\frac{3}{640}\left( 1-10 \delta +9\delta^2 \right) M^4 \right] \]

Where: \[ \delta=\frac{P}{P_0} \]

Where P₀ is sea level air pressure, 101325Pa. Obviously you can determine Mach number, M and equivalent airspeed, EAS from the previous equations.

The table below gives examples of all the airspeeds for both an airliner and helicopter calculated using the equations.

Aircraft	Altitude/ft	Temperature(T)/C	Density(ρ)/kgm^-3	Pressure(P)/Pa	True Airspeed(TAS)/kts	Mach No(M)	Equivalent Airspeed(EAS)/kts	Calibrated Airspeed(CAS)/kts
Airliner	35000	-55	0.380	23841.7	461	0.8	256.6	271.8
Helicopter	2000	11	1.155	94212.8	130	0.198	126.2	126.2

Values for pressure, temperature and density are calculated from ISA standard atmosphere, see the earlier article on ISA atmosphere [1]. The standard atmosphere can be corrected to estimate for non standard atmosphere conditions if the temperature deviation is known. Therefore the equations and mechanical flight computers can be used to estimate airspeed conversions for non standard atmosphere conditions.

Pilots use a mechanical flight computer such as the CRP-5 or similar to convert airspeeds, in larger more complex aircraft the airspeeds will be calculated by the air data computer (ADC).

A mechanical flight computer such as the CRP-5 can calculate both Mach number and calibrated airspeed (CAS). As equivalent airspeed (EAS) is nearly equal to calibrated airspeed (CAS) at low speed pilots tend not to consider it.

Using the values for temperature and altitude in the table above for the helicopter example, on CRP-5 you align the altitude and temperature in the airspeed window and read the corresponding values for true airspeed (TAS) on the outer scale and calibrated airspeed (CAS) on the inner scale. See picture below for a clearer understanding and to confirm the CRP-5 gives the same values given by the equations in the table.

Example of using CRP-5 to find helicopter CAS

To calculate Mach number using the CRP-5 is a bit simpler, you only need temperature. In the airspeed window you spin it round until the arrow with mach number beside it appears and align the arrow with the temperature. Then read the corresponding values for true airspeed (TAS) on the outer scale and Mach number on the inner scale. See picture below for more clarity and to confirm the CRP-5 gives the same values given by the equations in the table.

Example of using CRP-5 to find helicopter Mach No

Using the CRP-5 to calculate TAS and CAS for the airliner example is similar to the process for a helicopter but slightly more complicated as you have to make an adjustment for compressibility for true airspeeds (TAS) over 300 kts. You follow the same process as was done in the helicopter example only with the airliner values. Then use the formula at the compressibility correction (comp. corr.) window as given below:

\[ \frac{TAS}{100} -3\]

The formulae would give you (461/100) - 3 = 1.61, which means you must increase the value from 39 to 40.61 approximately in the 'comp. corr.' window. Then as before read the corresponding values for true airspeed (TAS) on the outer scale and calibrated airspeed (CAS) on the inner scale. See picture below for more clarity and to confirm the CRP-5 gives the same values given by the equations in the table.

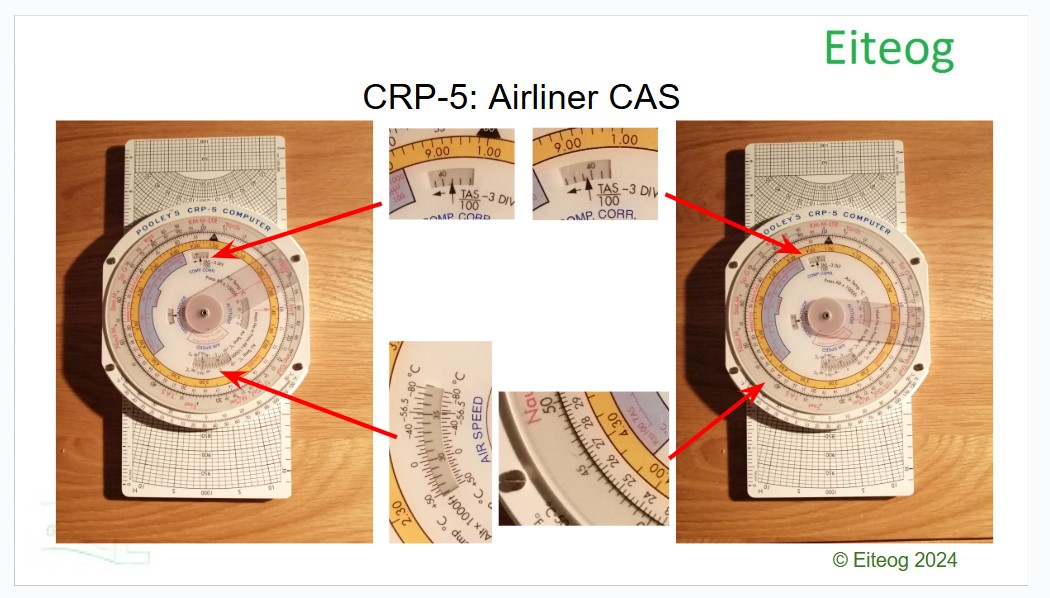
Example of using CRP-5 to find Airliner CAS

Using the CRP-5 to calculate Mach number from TAS for the airliner example is exactly the same as in the helicopter example obviously using airliner values from the table for temperature, TAS, etc. As before see picture below for more clarity and to confirm the CRP-5 gives the same values given by the equations in the table.

Example of using CRP-5 to find Airliner Mach No

As you can see from the above examples the indicated airspeed (IAS) does not differ greatly from true airspeed (TAS) for helicopter operations so therefore a helicopter pilot can assume they are the same for normal flying operations however, an airliner pilot cannot and must convert their IAS to TAS.

Airspeed conversions is only one of the many functions a mechanical flight computer such as the CRP-5 can perform, if you are interested in seeing more content on the use of a mechanical flight computer such the CRP-5 make sure you let me know via comments on facebook or email. For more information on airspeed conversions see references [2] and [3].

Please leave a comment on my facebook page or via email and let me know if you found this blog article useful and if you would like to see more on this topic. Most of my blog articles are on:

Mathematics
Helicopters
VTOL UAVs (RC Helicopters)
Sailboat Design and Boatbuilding

If there is one or more of these topics that you are specifically interested in please also let me know in your comments this will help me to write blog articles that are more helpful.

References:

[1] http://www.eiteog.com/EiteogBLOG/No13EiteogBlogISA.html

[2] Aircraft Performance & Design, John D. Anderson Jr., 1999, McGraw Hill

[3] Aircraft Performance (Cambridge Aerospace Series, Series Number 5), W. Austyn Mair, David L. Birdsall, 1996, Cambridge University Press

Disclaimer: Eiteog makes every effort to provide information which is as accurate as possible. Eiteog will not be responsible for any liability, loss or risk incurred as a result of the use and application of information on its website or in its products. None of the information on Eiteog's website or in its products supersedes any information contained in documents or procedures issued by relevant aviation authorities, manufacturers, flight schools or the operators of aircraft, UAVs.